Context

During a redteam assessment for one of our client, we had the opportunity to look into Fortigate SSL VPN, one of the most used VPN solution worldwide. We discovered a heap overflow bug on the internet-facing interface of the VPN. This vulnerability, which is reachable without authentication, can be leveraged to get remote code execution on Fortigate instances. CVE-2023-27997 was assigned, with a CVSS of 9.2 (but really, it's a 10). We believe the bug has been present for a long, long time (more than on the 7.x and 6.x branches). Please refer to FG-IR-23-097 for details about affected versions.

We'll describe here the bug and the exploitation process on two architectures, along with a few pointers for blue teamers.

The bug

The bug is located on the web interface that allows users to authenticate to the VPN. This interface is, by design, internet-facing. If we hit the path /remote/hostcheck_validate, we can send an HTTP parameter named enc, through GET or POST. The parameter, which does not seem to be much used now, seems to be an old way for Fortigate to forward HTTP parameters across requests.

The enc parameter is a structure containing a seed, size (2 bytes) and data. Both size and data are encrypted.

The seed, stored as 8 hexadecimal characters, is used to compute the first state of a XOR keystream:

$$S_0 = MD5(salt | seed | ``\text{GCC is the GNU Compiler Collection.}'')$$

salt is a random value created by the server, which can be retrieved by issuing a GET request to /remote/info.

The other states of the keystream are computed like so:

$$\begin{matrix} S_1 = MD5(S_0)\\ S_2 = MD5(S_1)\\ S_{n+1} = MD5(S_n)\\ \\ S = S_1 | S_2 | S_3 | ... | S_n\\ \end{matrix}$$

The keystream $S$ can be xored to the rest of the enc payload, the size and the ciphertext, to decrypt them. It is sent as an hexadecimal string.

The decryption method looks like this (simplified code):

int parse_enc_data(char *in)
{
    int in_len = strlen(in);
    int given_len;
    int xored_given_len;

    if(in_len & 1)
    {
        return 1;
    }

    compute_key_zero(salt, in, 8, md5); // [1] Computes key from salt, seed

    out = alloc_block(*pool, (in_len >> 1) + 1); // [2] Allocate a buffer
    unhex(out, in); // [2] Hexa-decode in to out

    if (out[0]) // first byte of seed must be 0x00
    {
        ap_log_rerror((__int64)a1, 8LL, (__int64)"invalid encoding method %d\n", needs_null);
        return 1;
    }

    // [3] Decrypt given length
    xored_given_len = *((_WORD *)out + 2);
    given_len = (unsigned __int8)(xored_given_len ^ md5[0]);
    BYTE1(given_len) = md5[1] ^ HIBYTE(xored_given_len);

    if ( inlen - 5 <= given_len ) // [4] Verify bounds
    {
        ap_log_rerror(a1, 8LL, "invalid enc data length: %d\n", given_len);
        return 1LL;
    }

    // [5] Decrypt: xor every input from byte 6 (4 bytes for seed, 2 bytes for length)
    p = &out[6];
    if (given_len)
    {
        int i = 0LL;
        while (i < given_len)
        {
            p[i] ^= md5[(i + 3) % 16];
            if ((i + 3) % 16 == 0) // Current state is exhausted: compute new
            {
                MD5_Init(md5_ctx);
                MD5_Update(md5_ctx, md5, 16LL);
                MD5_Final(md5, md5_ctx);
            }
            ++i;
        }
    }
    out[6 + given_len] = 0; // [6] Append null byte

    add_kvp_to_hashmap(a1->params, out); // [7] Process plaintext

    // Allocated buffers get freed at the end of the HTTP exchange
    return 0;
}

The function behaves like so:

1. Compute an MD5 (16 bytes), which is the first state of the key from the salt and the seed (first 8 chars of in)
2. Allocate a buffer of size in_len / 2 + 1, out, and hexadecimal-decoded input into it
3. Compute the length given by the user, given_len, by xoring the first two bytes of the payload with the first two of the key
4. Bound check: verify that the given length is not greater than the size of the buffer
5. Decrypt the whole string in place: XOR the first 14 bytes, then compute a new state $K_1$, use it to XOR the 16 next bytes, and repeat.
6. Put a NULL byte at the end of the decrypted data
7. Add decrypted values to the hashmap containing HTTP input params

The bug is easy to spot: when the program checks that the given length is not greater than the length of the sent payload, it compares in_len to given_len. But while the former describes the length of the payload in hexadecimal (e.g. '41424343'), the latter describes its size in raw bytes (e.g 'ABCD'). As a result, given_len can be twice as big as it should be.

This bug allows us to apply the decryption process to not only to the ciphertext in out, but also to the memory that comes after.

This makes for a funny bug: instead of just overwriting bytes in the heap, we get to XOR them with some MD5!

Exploit theory

The bug allows us to allocate a chunk of arbitrary size $N$, out, and then XOR bytes after the buffer with a keystream of MD5 hashes, for which we partially control the key. We control the size of the allocated buffer, and the size of the XOR overflow. In addition, the last byte of the overflow gets nulled.

Hereafter, we name $B_i$ the i^th byte in memory, and $K_i$ the i^th byte of the keystream. Therefore, triggering the bug with a length of $L$ applies:

$$\begin{cases} B_i \colonequals B_i \oplus K_i \enspace \text{with} \enspace i \in [0, L-1]\\ B_L \colonequals 0 \end{cases}$$

We "control" the MD5 hashes because we partially control the bytes used to create the first one:

$$\begin{cases} S_0 = MD5(salt | seed | \text{''GCC is the GNU Compiler Collection.''})\\ S_{n+1} = MD5(S_n)\\ S_n = K_{8 \times n} \enspace \text{to} \enspace K_{n \times 8+7} \end{cases}$$

It's easy to enforce the value of some bytes of the keystream by bruteforcing with the seed. We can't, however, hope to control all of it.

First idea

The first thing that comes to mind, is xoring the LSB of some address to change its position. Something like this:

00 C9 12 32 BB 7F 00 00 (0x7FBB3212C900) [Original pointer]
30 63 00 00 00 00 00    (0x000000006330) [Part of keystream]
----------------------- XOR
30 AA 12 32 BB 7F 00 00 (0x7FBB3212AA30) [Modified pointer]

However, this is costly: we need to find an MD5 hash which starts with 306300000000. This hash is the hash of another one, which is the hash of another one, etc. If the distance from the hash to the pointer we want to modify is 0x1000 for instance, this would be the 256th state of the key stream. Not to hard to compute once, but to bruteforce...

Even if we manage to get such a hash, the data previous to this modified pointer would get garbled, because it'd be XORed with previous hashes, whose contents we cannot choose.

jemalloc: some allocator

As it sounded pretty hard to get anything working, we took a look at the underlying allocator, to see if there were any way to leverage the bug.

The underlying heap, jemalloc, was unknown to us at the time. We were in a hurry (understand: I ragequit when trying to make shadow work) and not looking to acquire a deep understanding of it. Here's what we learned about it:

• Heap metadata is stored independently; you can safely overflow from one chunk (region) to another
• You can easily get contiguous allocations (after filling holes)
• There is some kind of LIFO mechanism on allocations of the same size: freeing a chunk of size $N$ and allocating the same size yields the same pointer.

The last point actually makes the exploitation very much easier: we can allocate the buffer we overflow from, out, at the same address, repeatedly.

A powerful primitive

Triggering the bug once makes it look like a bad primitive.

However, since we can consistently allocate the out buffer at the same spot in memory, several times, the primitive becomes very good. Indeed, we know that applying the same XOR twice to a value leaves it unchanged:

$$B_i \oplus K_i \oplus K_i = B_i$$

If we were to trigger the bug twice, with exactly the same parameters (seed and length), and if the two out buffers were allocated at the same memory address, each byte in the overflow would get XORed twice with the same value. We'd have completely unchanged memory, except for one byte which would be set to NULL. An improvement: a way to set a byte to zero, with no side effects.

Moreover, triggering the bug twice with the same seed, only the first time setting the length of the overflow to $L$, and the second time to $L+1$, yields even better results.

On the first iteration, we would have completely messed up data until the byte at offset $L$, which would be NULL. On the second iteration, every byte would get xored with the key twice, and thus become its old self again, except for $B_L$, which would take the value of $K_L$, as $0 \oplus K_L = K_L$. Byte $L+1$ would become NULL. We'd have:

$$\begin{cases} B_i \enspace \text{unchanged with} \enspace i \in [0, L-1]\\ B_L = K_L\\ B_{L+1} = 0 \end{cases}$$

So, to give byte $L$ an arbitrary value $X$, we can just compute a keystream such that $K_{L} = X$, and apply the primitive twice, once with length $L$, and once with length $L+1$.

Here's an example: we want to set $B_{5000}$ to $0x50$. We compute a seed such that $K_{5000} = 0x50$. This is the 8^th byte of the 250^th state, so $S_{250}[8] = 0x50$. If for instance the salt is $\text{e0b638ac}$, we can use the seed $\text{00690000}$ to get:

$$S_{250} = \text{917be51232917698\textcolor{red}{50}41ff4c5d50126e}$$

We then apply the primitive with length 4999. We get the following:

We apply it a second time, with length 5000:

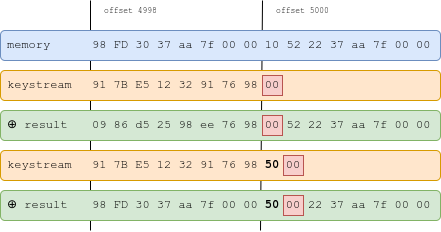
The memory is unchanged, except byte $5000$, which now has value $0x50$, and $5001$, which is now NULL.

Here's a good primitive: we now have a way to edit bytes in memory.

Improving efficiency

We can actually do better, and overwrite several bytes in a row, with one request per byte! Say we want to write ABC\0 in memory, $L$ bytes after the overflowed buffer. We first compute a seed $s_0$ such that $K^{s_0}_{L+2} = `C'$. Then, we compute a seed $s_1$ such that:

$$K^{s_1}_{L+1} = `B' \oplus K^{s_0}_{L+1}$$

and $s_2$ such that:

$$K^{s_2}_{L} = `A' \oplus K^{s_1}_{L} \oplus K^{s_2}_{L}$$

We then exploit by setting the first byte to zero (length: $L$):

$$\begin{cases} B_{L} = 0\\ B_{i} \enspace \text{unchanged with} \enspace i \ge L-1\\ \end{cases}$$

We then apply the primitive with the seeds in the reverse order, $s_2$ to $s_0$, with length $L+1$ to $L+3$. We get, for $s_2$:

$$\begin{cases} B_{L} = 0 \oplus \text{'A'} \oplus K^{s_1}_{L} \oplus K^{s_2}_{L}\\ B_{L+1} = 0\\ B_{i} \enspace \text{unchanged with} \enspace i \ge L+2\\ \end{cases}$$

Then, for $s_1$:

$$\begin{cases} B_{L} = 0 \oplus \text{'A'} \oplus K^{s_1}_{L} \oplus K^{s_2}_{L} \oplus K^{s_1}_{L}\\ B_{L+1} = 0 \oplus \text{'B'} \oplus K^{s_1}_{L+1}\\ B_{L+2} = 0\\ B_{i} \enspace \text{unchanged with} \enspace i \ge L+3\\ \end{cases}$$

And finally, for $s_0$:

$$\begin{cases} B_{L} = 0 \oplus \text{'A'} \oplus K^{s_1}_{L} \oplus K^{s_2}_{L} \oplus K^{s_1}_{L} \oplus K^{s_0}_{L} = \text{'A'}\\ B_{L+1} = 0 \oplus \text{'B'} \oplus K^{s_1}_{L+1} \oplus K^{s_1}_{L+1} = \text{'B'}\\ B_{L+2} = 0 \oplus \text{'C'} = \text{'C'}\\ B_{L+3} = 0\\ B_{i} \enspace \text{unchanged with} \enspace i \ge L+4\\ \end{cases}$$

Using the primitive 4 times, we managed to write ABC in memory! This technique has, however, a huge let-off, as it messes up everything that comes before the modified memory. For the rest of the blogpost, we'll stick to the initial technique, which requires 2 requests to set one byte.

Exploit practice

Now that we have a decent primitive, we need to find something to overwrite.

Target of choice: SSL

In 2019, Meh Chang and Orange Tsai exploited a heap overflow on the same binary, and chose to modify a structure named SSL. This kind of structure is allocated whenever a client connects to a worker process of sslvpnd, and gets destroyed when the client or the server closes the socket.

This is a perfect target for us.

First, because our primitive requires us to trigger the bug multiple times, and we need to attack a heap structure that persists accross HTTP requests.

Second, because the structure contains a callback handler, handshake_func. Due to the binary not being PIE, we can modify the value of this function pointer, and force the socket to perform an SSL handshake. From there, a standard stack pivot into whatever gets us a nodejs shell (there's no sh!).

To setup the heap, we'd need to have an empty chunk right before some SSL structure associated with a socket we control.

Attacking on 64 bits

Our test environment was a VM running on Intel 64 bits. The SSL structure has a size of 0x1db8 bytes, so it is allocated in a 0x2000-byte region.

Right before the allocation of the SSL structure, a buffer of size 0x2000 also gets allocated, in order to store the raw HTTP request sent by the client. With an unfragmented heap, the buffer sits on top the SSL structure in memory. This is where we'd like to have out! Luckily, if a client sends a request which is larger than 0x2000 bytes, the program reallocates the buffer, leaving the region empty. As the allocator is LIFO, and we control the size of out, this makes for a very clean exploit:

Create lots of sockets to the HTTPd service (fills gaps):

Send a huge HTTP request on the last socket, to force the buffer to be reallocated:

Use another socket to exploit the vulnerability; out gets allocated right where we need it:

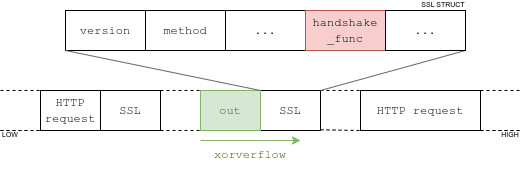
As the sslvpnd binary is huge, the ROP chain is not too hard to build. It is left as an exercise to the reader.

Note: schemas greatly inspired from this one.

Attacking on 32 bits

We discovered a while later that there were Fortigate builds for 32-bit architectures, such as ARM. Our redteam target was running on such a processor. In 32 bits, the SSL structure is basically half the size as it is in 64 (it is mostly made of pointers), so it gets allocated in regions of size 0x1000. The heap setup aforementioned does not work.

We are, however, extremely lucky: in addition to the 0x2000 buffer, the program allocates a 0x1000 buffer to store... the HTTP response. Which also gets reallocated, when too big. Without too much trouble, we were able to find a web page that echoes back some input, resulting in a 32-bit exploit:

• Create lots of sockets to the HTTPd service (fills gaps)
• Take the last connexion, and a request with a huge POST parameter
• The parameter gets echoed, forcing the reallocation of the HTTP response buffer
• Use another socket to exploit the vulnerability: the overflowed buffer gets allocated right were we need it.

ROPchain left as an exercice, again.

A few notes for red teamers

We're withholding the notes until a later date.

A few notes for blue teamers

We believe that providing as much details as we can on the vulnerability will allow you to better understand and protect against it.

Crash or no crash ?

As with all binary exploits, a crash is possible. You might notice in your logs crashes of the /bin/sslvpnd process. However, with proper exploits, you will not detect any.

Indicators

The bug is exploitable by issuing GET/POST requests to any of the two URLs: /remote/hostcheck_validate, and /remote/logincheck. Simple exploits will require several HTTP requests in quick succession to any of these URLs. It is however possible to make the exploit slower, by carefully setting up the heap.

Post-exploitation

It is possible for the attacker to live exclusively in memory, without modifying anything on the disk. Although reboots might remove in-memory payloads, there are ways to attain persistence on the appliance. The best way to protect yourself is to PATCH.

Demonstration

The video shows the first exploit we built, targeting x64:

And the second, targeting ARM, more efficient:

Conclusion

The vulnerability was patched by Fortinet on June 8^th, 2023 with versions 7.2.5, 7.0.12, 6.4.13 and 6.2.15, after being reported early in April. Their response was prompt and cordial. We remain however doubtful they ever ran a proper security assessment on the appliance, considering the number and quality of vulnerabilities that were found from 2019 to today.

Update: fixed the description of the bug, which mentioned a int8 comparison, which was wrong. The decompiler output was incorrect. Thanks bestswngs.